Influence of non-votersInfluence of non-voters on electoral outcomes
1. Introduction
Non-voters are often
the largest group in the electorate
and this is considered a problem in
the public and also by many social
scientists (Lijphart 1997). An
analytic question raised by the
debate on the importance of
non-voting is stated by Bernhagen
and Marsh (2007: 548): ‘If turnout
was 100 percent, would it affect the
election result?’ One answer to this
question can be given by a statistic
proposed by Kohler and Rose (2010).
The index calculates the proportion
of votes the runner-up party would
have to win among the non-voters in
order to change hands with the party
who gains the plurality of votes (hereafter:
the “winner”). If this
Kohler-Rose-Index is higher than
100%, it would be impossible for the
runner up to catch up the winning
party by gaining votes from the
non-voters. This website documents the calculation of the Kohler-Rose-Index and provides datasets and graphical displays of it for
See Kohler et al. (2012) for further details of the contents of the website.
2. Derivation of the Kohler-Rose-Index
Let W and R be
the absolute numbers of valid
votes of the winning and
runner-up party respectively,
and L be the absolute numbers of
non-voters that could have
participated in the election (i.e.
the Leverage). Assume that the
proportion of the non-voters who
vote for the runner up party
would be p. Then, the new number
of votes for this party will be
Assume further that the winning party and the other parties hold their relative proportions, w and o, among the non voters left behind by the runner up parties. Under this condition the number of votes for the winner will become
Setting the difference between (2) and (1) to zero, and solving for p leads to the following formula for the tipping point (i.e. the Kohler-Rose-Index):
Important Note: The formula above differs slightly from the formula published by Kohler and Rose (2010). In the original publication the sum of the vote proportions of the winner, the runner up party, and the other parties could be above 1 even for p<1. The formula here corrects this. Effectively pKR tend to be slightly higher with the new formula, especially if there are many voters for other parties.
3. Further assumptions used In the formula for the Kohler-Rose-Index there is the unknown quantity of available non-voters, L. Conceptually, the number of available non-voters is equal to the maximum turnout minus the observed valid turnout, with maximum turnout being the highest possible turnout. Kohler and Rose (2010) argue that the highest possible turnout cannot be 100% for a number of reasons. They therefore use 100% - Absent electors (9.1%) - Invalid votes (4.8%) = 86.1% as maximum turnout. While setting up the data base for this web-page it has turned out, however, that several elections had a higher turnout than 86.1. Maximum turnout has been therefore set to 96%, which is slightly above the highest valid turnout observed in the data (Malta 1990: 95.5%).
4. Derived statistics for the likelihood of change
The graphical displays show the actual vote proportion of the runner-up party together with the Kohler-Rose-Index. The more the two numbers deviate, the lower the likelihood that winner and runner-up could change hands due to the participation of non-voters. The downloadable datasets and tables also list two additional statistics that incorporate that idea:
The higher Dabs and Drel are, the lower is the likelihood of change due to non-voters. Note that we propose the following terms to describe the likelihood of change:
5. Data sources The data for calculating the Kohler-Rose-Index for the German federal elections and the German state elections has been taken from Statistisches Bundesamt (2005) and the website of the German Federal returning officer
References Bernhagen, P., Marsh, M., 2007. The partisan effects of low turnout: Analyzing vote abstention as a missing data problem. Electoral Studies 26, 548–560. Kohler, U., Rose, R., 2010. Under what circumstances could maximizing turnout alter an election result? Representation 46 (2), 119–138. Lijphart, A., 1997. Unequal participation: Democracy’s unresolved dilemma - presidential address 1996. American Political Science Review 91 (1), 1–14. Statistisches Bundesamt, 2005. Endgültiges Ergebnis der Wahl zum 16. deutschen Bundestag am 18. September 2005. Wirtschaft und Statistik 11/2005, 1153–1167.
|


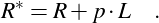 (1)
(1) (2)
(2)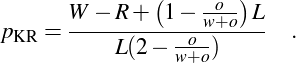 (3)
(3) This expresses Dabs in terms of a proportion of the actual vote share of the runner-up party.
This expresses Dabs in terms of a proportion of the actual vote share of the runner-up party.